Plot Linear Regression R Math

The shaded area around the regression line illustrates the variance. Height c 176 154 138 196 132 176 181 169 150 175. In this topic we are going to learn about multiple linear regression in r.

conversion sheets for chemistry math ln ln math why is place value important math asvab practice test math printable roman numerals to arabic math study for ged online for free math simplifying radicals calculator math subtracting improper fraction calculator math

Linear Regression With Go For A Long Time Now I Have Been By Marc Guasch Devthoughts Medium

Chapter 7 Correlation And Simple Linear Regression Natural Resources Biometrics

Introduction To Residuals And Least Squares Regression Video Khan Academy

Linear Regression For Predictive Modeling In R

Linear Regression Using Desmos Youtube

Estimating With Linear Regression Models Video Khan Academy

Local Regression Wikipedia

8 1 A General Strategy For Modelling Nonlinear Regression Functions Introduction To Econometrics With R

Independence of observations aka no autocorrelation.

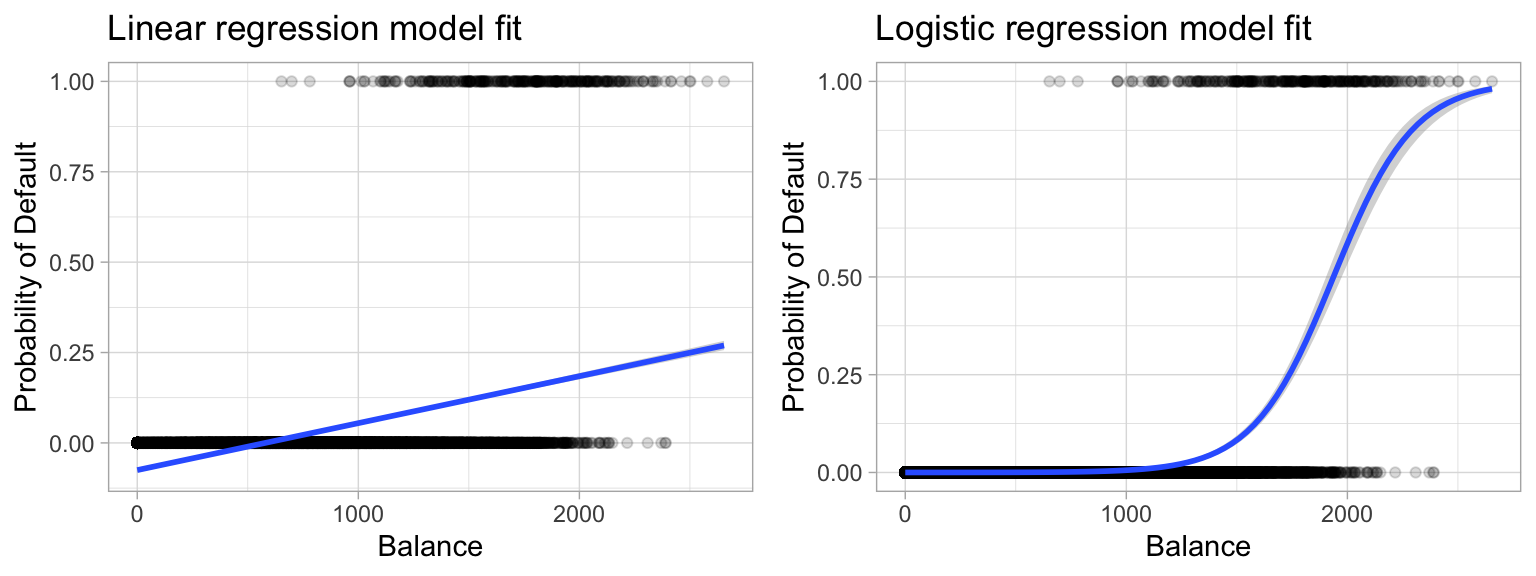
Plot linear regression r math. 2020 applied math statistics math majors. Now that we have seen the linear relationship pictorially in the scatter plot and by computing the correlation lets see the syntax for building the linear model. Qq plots are ubiquitous in statistics. Multiple linear regression is an extended version of linear regression and allows the user to determine the relationship between two or more variables unlike linear regression where it can be used to determine between only two variables.

Most people use them in a single simple way. Copy and paste the following code to the r command line to create this variable. Make sure your data meet the assumptions. From the article absorption of phosphate arsenate.

As you can see it consists of the same data points as figure 1 and in addition it shows the linear regression slope corresponding to our data values. Ggplot2 scatterplot with linear regression line and variance. The scatter plot shows a linear relationship between the phosphate absorption index. Because we only have one independent variable and one dependent variable we don t need to test for any hidden relationships among variables.

R language tutorials for advanced statistics. We take height to be a variable that describes the heights in cm of ten people. Multiple linear regression with r. Interpreting linear regression coefficients in r from the screenshot of the output above what we will focus on first is our coefficients betas.

Today let s re create two variables and see how to plot them and include a regression line. Figure 2 shows our updated plot. Beta 0 or our intercept has a value of 87 52 which in simple words means that if other variables have a value of zero y will be equal to 87 52. We can use r to check that our data meet the four main assumptions for linear regression.

You may also be interested in how to interpret the residuals vs leverage plot the scale location plot or the fitted vs residuals plot. Fit a linear regression model check if the points lie approximately on the line and if they don t your residuals aren t gaussian and thus your errors aren t either.